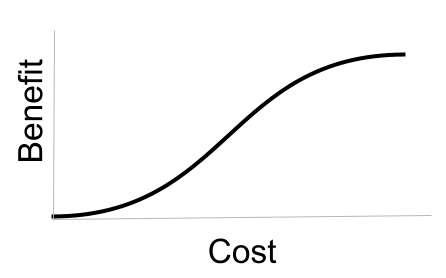
I’ve realized that I often stumble when explaining the concept of “marginal benefit”. I always have the image above in my head, but actually haven’t seen it too often displayed in the world. So I’m taking a moment to put it in the world, along with the implications of the mental model it represents:
- Start at the lower left. That’s the very moment that you undertake a project. Zero cost (dollars and hours) and zero benefit (the world has not changed one bit).
- Now imagine spending just the minimal amount, inching to the right along the curve, before walking away. It will have been a low-cost project. But it will still have almost zero benefit. If you’re thinking of starting a lemonade stand, that’s like spending 1 hour and $1 to buy lemons. If you do nothing else, your profit is the same as if you hadn’t started.
- If you keep moving, you start to see some benefit. Things get really exciting halfway across the curve. You’ve seen some definite benefit, and every bit of additional cost is returning a huge amount of benefit. That’s like spending 10 hours and $10 on actually buying ingredients and setting up your stand for a few days. You’ve got regular customers, and you’re selling as fast as you can make the stuff. Of course you’d spend the 11th hour and 11th dollar to keep going – the benefit is almost guaranteed.
- But to the far upper right, the potential benefit maxes out. If you’ve sold 7 billion glasses of lemonade, there are no more thirsty people anywhere on earth. Putting in additional time and money will have no impact at all.
Everyone gets this intuitively, but we don’t have good shared vocabulary around it. We definitely don’t have good vocabulary around the different ways that curve could be stretched and squeezed.